How to play?

The goal of the game is to reveal an image made up of small black squares (also called "pixels").

To do this, you must blacken the empty squares in which you are sure that a black square is present.

And in the same way, you must cross out the empty squares in which you are sure that no black square is present.

You have solved the picross when you have filled all the empty squares of the grid with black squares and crosses.

At the top of each column, and to the left of each row, are indicated one or more numbers.

These numbers are in fact an indication of the number of black squares stuck together, in the corresponding column or row.

For example, for the row above: The numbers 3 and 4 indicate that in this row of 10 squares, there are 3 glued squares, and that further to the right, there are 4 more glued.

The problem is that we do not know the exact position of these two portions composed of glued squares.

The only thing we are sure of is that these two portions cannot be glued together. Otherwise they would automatically transform into a single portion of 3+4=7. There is therefore at least a cross between the two, to separate them.

Based on this principle, the rule of the game is as follows:

You must solve the entire grid while respecting all the information in the columns and rows.

There are several techniques that allow you to deduce the presence of squares or crosses.

The first is to deduce the position of one or more squares on the rows and columns that contain enough squares so that the different possibilities "overlap".

If we take the example given previously, the different possibilities are as follows:

We can blacken the different positions in which there is always a black square, whatever the positioning of the portions.

Here's another simpler example of "overlapping":

When a square is located at the very beginning or end of a row or column, you can blacken the corresponding number of boxes and finish with a cross.

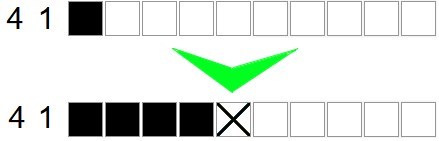
In the example below, the first number on the left is 4. So we blacken 4 boxes, then add a cross after them, to finish the portion.

When there is only one number in the row or column information, you can cross out the boxes that are too far from an existing square.

In the example below, the boxes that are more than 3 boxes away from the existing square cannot contain a square. They are therefore crossed out.

When a square is near the beginning or end of a row or column, and the corresponding number is large enough to exceed its position, then you can blacken the boxes that exceed it.

In the example below, the first portion on the left is 4 boxes long, and since it cannot be located further left than the beginning of the row, you can blacken the boxes that exceed it just after the black box already present.

When a portion is too large to be placed at the beginning or end of a row or column, because of the presence of a cross. Then you can cross out the corresponding empty boxes.

In the example below, the portion that measures 3 boxes cannot be positioned at the beginning of the row. We can therefore cross out the entire beginning of the row until reaching the cross already present:

When there is only one number in a column or row, and the crosses are too close together for the portion to fit between them, then you can cross out the boxes in the interval.

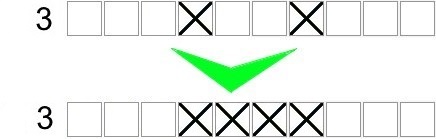
In the example below, the portion of 3 boxes cannot fit between the two crosses already present. So you can cross out the two boxes between the two crosses.

When there is only one number in a column or row, and several squares are separated, then you can connect them together.

In the example below, part of the portion that measures 4 squares is necessarily located between the two squares already present. We can therefore blacken the square located between the two.

When there is only one possibility, you can complete the entire row or column (see the different examples):

In the example below, the entire row is empty. So we can fill it with crosses:

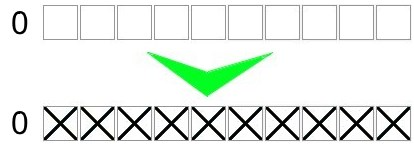
In the example below, the entire row is full. So we can fill it with squares:

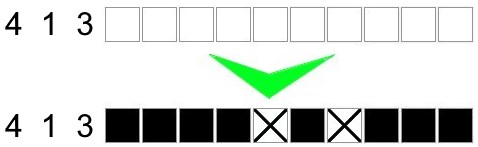
In the example below, the sum of the lengths of the different portions + the separating crosses is equal to the length of the row:

4 squares + 1 cross + 1 square + 1 cross + 3 squares = 10 boxes

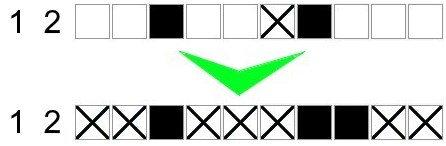
In the example below, all the portions are positioned. So we can complete the entire row:

Below is the animation of a complete solving:

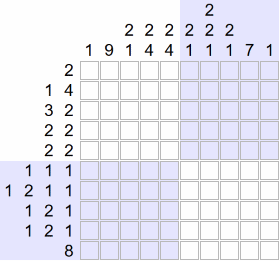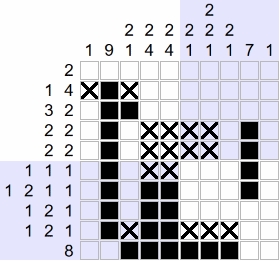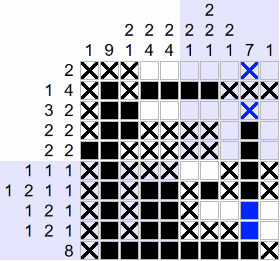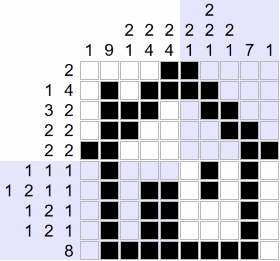
If you want to see the detail of this solving, step by step, visit the following page: